昨天我們探討了光通過單狹縫後在屏幕上形成的光強圖案，考慮了狹縫寬度和光波長等物理參數。

今天我們從另外一個角度——一維傅立葉變換 Φ(kx ) 分析任何空間或時間函數。

兩者差異在於：
單縫繞射公式的結果則是一個實數值函數 I(θ)，表示光強隨著角度 θ 的變化。
一維傅立葉變換的結果是一個複數函數 Φ(kx )，代表頻域中的振幅和相位。

一維傅立葉變換公式如下：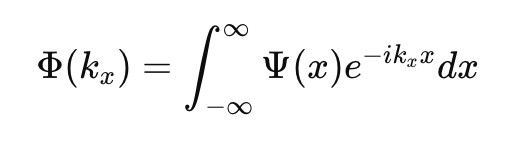

import numpy as np
import matplotlib.pyplot as plt

#Define single slit 單純穿slit的光
def single_slit(x, d): #d=slit width
    if -d/2 < x < d/2: #光如果落在slit中間
        return 1/d #為了乘以d後通過狹縫面積好算為1，先除以d
    else:
        return 0 #落在狹縫外
    
D = 10 #繪圖範圍-5~5
d = 1  #狹縫寬度
N = 501 #繪圖間隔（精度）
x_list = [-D/2 + D*i/N for i in range(N)] #X=0~500去切繪圖範圍，從-D/2慢慢畫到D/2
source = [single_slit(x_list[i], d) for i in range(N)]  #把光源帶進函數

def phase_term(kx, x): #處理complex，也就是公式中dx以前的部分
    phase = complex(0, -kx*x) #前面放實部（這裡面沒有，所以為0），後面為虛部-kx*x
    return np.exp(phase) #呼叫exponential e的i次方

def Fraunhofer_1D(kx, source, x_list, dx): #dx就是D/N(寬)，source帶入phase term就是每段高度做積分
    output = 0
    for i in range(len(x_list)):
        rec_area = source[i]*phase_term(kx, x_list[i])*dx #黎曼和長方形面積
        output += rec_area  #不斷地跑回圈加長方形面積
    return output

K = 2*np.pi*N/D #波數
kx_list = [-K/2 + K*i/N for i in range(N)] #波數list(空間上的分佈)
far_field = [Fraunhofer_1D(kx_list[i], source, x_list, D/N) for i in range(N)] #把切好的波數分佈帶入formula，其他項目依序帶入 


plt.plot(x_list, far_field)
plt.show()

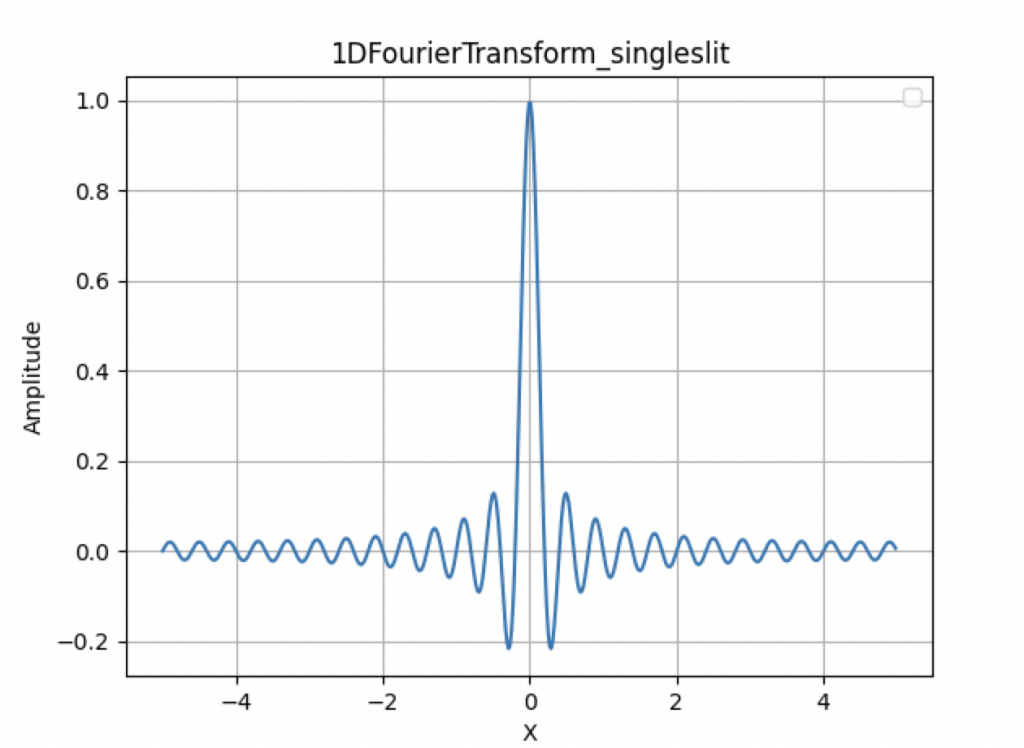
同樣是單狹縫繞射，今天試了不同的公式，python編程是光電半導體課程學程助教教的，chatGPT這次主要在協助我理解公式組成，以及和光強度公式的差異。

今天就先到這，明天繼續！